本篇文章是要記錄在機器學習當中常見的「群集分析」(Clustering,又稱「分群」、「聚類」分析)方法。機器學習演算法當中概略分為兩大類:「監督式學習」和「非監督式學習」。非監督式學習即是指資料沒有標籤(unlabeled data)或沒有標準答案,無法透過所謂的目標變數(response variable)來做分類之訓練,群集分析又是非監督式學習的代表。
針對群集分析的文章將會依序提到以下內容,並且會拆成上下兩篇文章分別介紹。本篇文章會先介紹前三項,後三項則收錄於第二篇文章。本文的重點在於簡介這些分群演算法的主要差異,並補充其 R 或者 Python 實作的範例,但不會提及這些分群演算法的數學方程式推導。
1. 群集分析的主要功能
2. 「階層式分群」與「切割式分群」
# 階層式分群 Hierarchical Clustering
階層式分群透過一種階層架構的方式,將資料層層反覆地進行分裂或聚合,以產生最後的樹狀結構圖(又稱作 dendrogram),再選取最佳的群聚數,故並不需要預設分群數目。其常見的方法有兩種:
缺點:通常只適用於少量資料,很難處理大量資料。
# 切割式分群 Partitional Clustering
相對於階層式分群,切割式分群將所有資料都視為「同一層」,因此不會有分層的樹狀結構。其透過預先指定群的數目後,再用一套疊代的數學運算法,找出最佳的分群方式以及相關的群中心。以下要逐一介紹的 K-means、K-medoids、K-modes、Spectral Clustering、Expectation-Maximization Clustering、Gaussian Mixture Model、OPTICS Clustering、Fuzzy Clustering、Gray Clustering 等等,皆屬於切割式分群。
參考資料與 R & Python 程式碼範例:
3. K-means 與它快樂的朋友們
# K-means
大概是知名度最高的分群演算法。
# K-medoids
為了解決 K-means 容易受到極端值影響的問題,於是便有了 K-medoids。
# K-modes
前兩種分群演算法都聚焦在數值型資料,那如果遇上類別型資料怎麼辦?於是我們有了 K-modes。其搜尋群聚中心的方法是以各類別資料的眾數(Modes)為依據,因此解決了前兩者無法解決類別型資料的問題。
# K-prototype
那麼,如果資料集當中同時包含有數值型資料與類別型資料的?那就把 K-means 和 K-modes 混在一起做撒尿牛丸吧!其是透過設定了一個目標函數,透過不斷迭代運算,直到目標函數值不變。目標函數當處理數值型資料的方式和 K-means 一樣,不同的距離計算方式,會帶來不同的分群結果。
小結
K-means 家族當中,哪一種最演算法最優呢?當然是看要處理的問題目標、資料的類型、資料量的小,以及有多少時間可以來解決問題而定。
此外,有個知名的監督式學習分類演算法,叫做 kNN(k Nearest Neighbor,「k 鄰近」演算法),它跟 K-means 家族的分群演算法是不同的東西。
參考資料與 R 程式碼範例:
針對群集分析的文章將會依序提到以下內容,並且會拆成上下兩篇文章分別介紹。本篇文章會先介紹前三項,後三項則收錄於第二篇文章。本文的重點在於簡介這些分群演算法的主要差異,並補充其 R 或者 Python 實作的範例,但不會提及這些分群演算法的數學方程式推導。
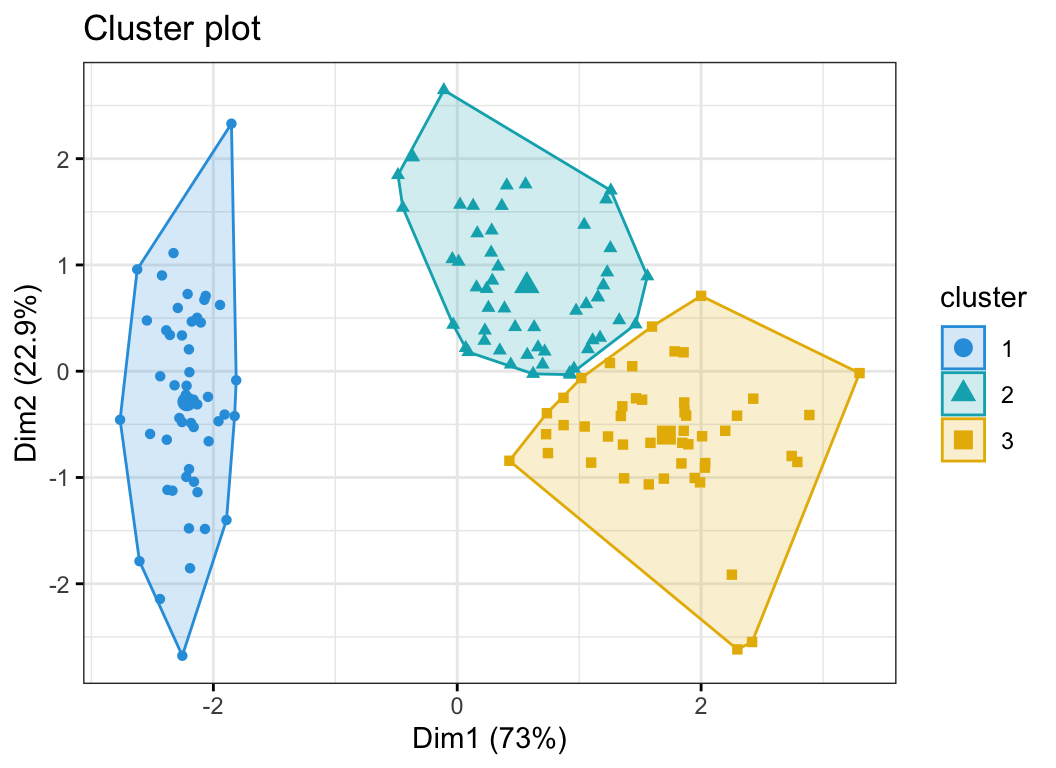
Photo credit : Datanovia
1. 群集分析的主要功能
2. 「階層式分群」與「切割式分群」
3. k-means 演算法及其變體
4. k-means之外的切割式分群演算法
5. 「剛性分群」與「柔性分群」
6. 如何決定最佳分群數?
1. 群集分析的主要功能
- 資料精簡、降低雜訊、降低計算量
- 推論假設的產生或驗證
2. 「階層式分群」與「切割式分群」
# 階層式分群 Hierarchical Clustering
階層式分群透過一種階層架構的方式,將資料層層反覆地進行分裂或聚合,以產生最後的樹狀結構圖(又稱作 dendrogram),再選取最佳的群聚數,故並不需要預設分群數目。其常見的方法有兩種:
- 聚合式階層分群法(Bottom-up, Agglomerative) : 如果採用聚合的方式,階層式分群法可由樹狀結構的底部開始,將資料或群聚逐次合併。
- 分裂式階層分群法(Top-down, divisible) : 如果採用分裂的方式,則由樹狀結構的頂端開始,將群聚逐次分裂。
- 概念簡單,可用樹狀結構來表現整個計算過程。
- 只需要資料點兩兩之間的距離,就可以建構分群結果,而不需要資料樣本的實際座標。
- 無論是數值或者類別的資料皆適用。
缺點:通常只適用於少量資料,很難處理大量資料。
# 切割式分群 Partitional Clustering
相對於階層式分群,切割式分群將所有資料都視為「同一層」,因此不會有分層的樹狀結構。其透過預先指定群的數目後,再用一套疊代的數學運算法,找出最佳的分群方式以及相關的群中心。以下要逐一介紹的 K-means、K-medoids、K-modes、Spectral Clustering、Expectation-Maximization Clustering、Gaussian Mixture Model、OPTICS Clustering、Fuzzy Clustering、Gray Clustering 等等,皆屬於切割式分群。
參考資料與 R & Python 程式碼範例:
- AI - Ch19 機器學習(7), 分群/聚類:階層式分群法 Clustering: Hierarchical Clustering | Mr. Opengate
- Hierarchical Clustering 階層式分群 | Clustering 資料分群 | R 統計
- Clustering method 4 (Hierarchical Clustering) - Taiwan AI Academy - Medium
- Clustering method 7 (BIRCH) - Taiwan AI Academy - Medium
3. K-means 與它快樂的朋友們
# K-means
大概是知名度最高的分群演算法。
- 其是透過計算每一筆資料之間的距離平均值(Means)平均值作為中心點(Centroid)來對資料進行分群。不同的距離計算方式,會帶來不同的分群結果。
- 在執行 K-means 時,其是隨機從資料集中挑選 k 個資料點當作初始中心點,因此每一次的執行結果可能不同
- 無論採用何種距離計算方式,其目標是都是最大化群內的相似度,同時最大化及群與群之間的相異度。
- 適用於數值型(Numeric)的資料。
- 優點是簡單容易執行,缺點是容易受到極端值(Outlier)的影響。
# K-medoids
為了解決 K-means 容易受到極端值影響的問題,於是便有了 K-medoids。
- 其是以每筆資料之間的中位數(Medoids)作為中心點來對資料進行分群,較不容易因為極端值而使結果產生偏誤。和K-means一樣,不同的距離計算方式,會帶來不同的分群結果。
- 由於演算法通常需要花較多的時間來搜尋資料之間的中位數,故在執行 K-medoids 所需要的時間跟運算資源也比較多,故比較適用於規模較小的資料集。
- 適用於數值型(Numeric)的資料。
# K-modes
前兩種分群演算法都聚焦在數值型資料,那如果遇上類別型資料怎麼辦?於是我們有了 K-modes。其搜尋群聚中心的方法是以各類別資料的眾數(Modes)為依據,因此解決了前兩者無法解決類別型資料的問題。
# K-prototype
那麼,如果資料集當中同時包含有數值型資料與類別型資料的?那就把 K-means 和 K-modes 混在一起做撒尿牛丸吧!其是透過設定了一個目標函數,透過不斷迭代運算,直到目標函數值不變。目標函數當處理數值型資料的方式和 K-means 一樣,不同的距離計算方式,會帶來不同的分群結果。
小結
K-means 家族當中,哪一種最演算法最優呢?當然是看要處理的問題目標、資料的類型、資料量的小,以及有多少時間可以來解決問題而定。
此外,有個知名的監督式學習分類演算法,叫做 kNN(k Nearest Neighbor,「k 鄰近」演算法),它跟 K-means 家族的分群演算法是不同的東西。
參考資料與 R 程式碼範例:
- K-means和K-medoids - IT閱讀
- 聚類分析之k-prototype算法解析 - 台部落
- RPubs - R筆記–(9)分群分析(Clustering)
- Partitional Clustering 切割式分群 | Kmeans, Kmedoid | Clustering 資料分群
- AI - Ch18 機器學習(6), 分群/聚類:K平均演算法 Clustering: K-means Algorithm | Mr. Opengate